Simulation work at SP3


3D Potential distribution across the plasma

SP3 has had a long history of involvement with computer modelling of plasma phenomena. In particular the development and use of Particle-in-cell (PIC) techniques for simulation of low pressure, low temperature, radiofrequency plasmas used in materials processing applications.

  1. Introduction
  2. Brief description of Particle-in-Cell techniques
  3. History of Simulation Usage in SP3
  4. Current Research in the Lab
  5. Some web publications


Return to SP3 Home Page

Introduction


The lab started using PIC in the mid 80s, shortly after the technique was adapted for bounded plasma systems by Ned Birdsall's group at University of California Berkley (for a history of PIC development see C.K. Birdsall (1991) IEEE Trans. Plasma Sci., 19, 65 ). The technique models charged species in the plasma, moving in the electric fields created by applied voltages and inter-particle coloumb forces. PIC codes also include collisions between charged species and background neutral gas atoms, and use boundary conditions which can include external LCR circuits. PIC is particularly adept at modelling non-equilibrium plasmas, in which the particle distributions are not solely a function of the local fields. They have been used to reproduce extremely accurately, experimental measurements of non-Maxwellian electron and ion distributions in both the bulk and at the reactor surfaces. PIC codes are widely used for modelling a variety of plasma types and conditions including rf systems, dc glow and magnetron discharges and plasma immersion ion implantation.

However, PIC is computationally intensive and are inherently subject to noise on the density and field distributions. This currently limits simulations to low pressure systems in which the plasma densities are less than 10^17 /m^3. Most PIC simulations are one dimensional for the same reason (although the use of faster numerical techniques and supercomputers has seen the development of higher dimensional codes). In this sense PIC techniques complement fluid methods, which deal well with coherent behaviour of bulk populations, but are not so useful for determining non-linear behaviour of small subgroups (for example the heating of a small fraction of the electron density in the sheaths). Hybrid models, which incorporate a combination of modelling techniques, are becoming increasingly common for more complete simulation of plasma processing systems, and may include plasma chemistry, plasma-wall interactions and the effect of magnetic fields.
As computers become faster some of the limitations of PIC simulations are being lifted.

Brief Description of Particle-in-cell Techniques

Charged plasma species (and possibly neutrals) are modelled as individual macro-particles (each macro-particle represents a large number of real particles). Particles move in the plasma using Newton's laws and self-consistently calculated electric fields resulting from applied voltages and inter-particle coloumb forces. PIC codes can include collisions between charged particles and background gas atoms, using Monte-Carlo techniques and (typically) a "null" collision scheme. In this scheme real cross-sections are used, together with a "pseudo" cross-section with a constant collision frequency. Ions/electrons are chosen for collision and then the collision type is determined: elastic, inelastic or "none".

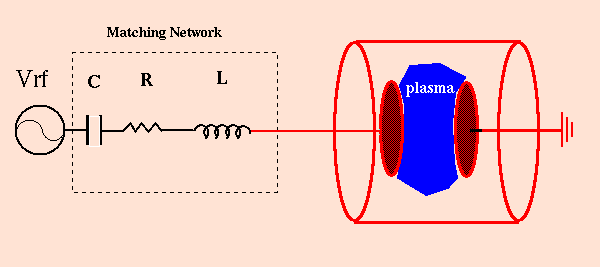
PIC codes can be bounded - including walls which determine boundary conditions for the potential solver - or unbounded. In bounded codes modelling plasma processing reactors the boundary conditions can also model external voltage/current sources and LCR "matching" circuits.


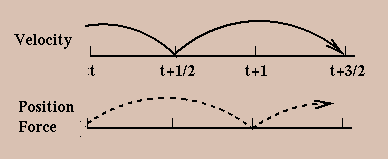
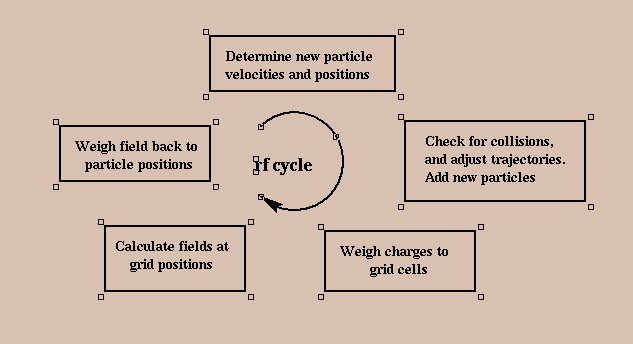
Schematic of a plasma reactor with an external matching circuit

Electric fields are solved self-consistently due to the superposition of external (applied) fields and internal fields from charge distributions. This is done by using a non-physical grid across the plasma (the "cell" part of the name) and determining the charge density at each grid position by assigning particles to the grid according to their position, and a weighting scheme. Once the charge density at the grid positions is known the potentials can be calculated using Poisson's equation. Then the electric fields at the grid can be determined and finally fields at the particle positions are determined using an inverse weighting scheme. Particles can then be moved via Newton's equations, using a leap-frog finite differencing method (positions and fields are calculated at integer time-steps, velocities at half time-steps).


Schematic of leap-frog differencing technique


Schematic showing algorithm for 1 time-step of the simulation

Some useful references:
C.K. Birdsall and A.B. Langdon "Plasma Physics via Computer Simulation", McGraw-Hill Book Company, Singapore (1985).
C.K. Birdsall, IEEE Trans. Plasma Sci., 19, 65-85 (1991).
T. Tajima "Computational Plasma Physics: with Applications to Fusion and Astrophysics" Addison-Wesley Publishing Co. (1989).

History of Simulation Usage in the Lab

1985
Initial development of an unbounded 1D electrostatic PIC simulation to study beam-plasma interactions

1988
Development of a bounded 1D simulation of a planar rf discharge modelling a hydrogen-like gas, used to study basic phenomena such as current/voltage relationships, density and potential distributions and sheath heating of the electrons.

1990
1D electrostatic PIC simulation of asymmetric rf discharges modelling hydrogen and argon gases with realistic cross-sections.
1992
Use of a 2D PIC/fluid hybrid simulation with flexible boundary conditions, to model inductive sources (including helicon reactors). Also used to look at diffusion of evaporant species through a plasma in a HARE-like reactor (refer to HARE )

1995
Modelling plasma breakdown and decay, in pulsed rf discharges,using both symmetric and asymmetric reactor geometries.

Current Research in the Lab


Currently the main area of interest for simulation research in the lab is modelling pulsed rf systems. The simulation is being used in conjunction with a small experimental experimental reactor in order to make a detailed study of breakdown and approach to equilibrium in a low pressure, capacitively coupled, rf argon discharge (see Pulsed Plasmas ). Studies have been made of the evolution of the bias voltage in asymmetric geometry, which indicates that previously unknown behaviour of the currents and plasma potential are involved (see "Charging of the blocking capacitor in an asymmetric discharge" for details ).

The simulation is also being used to investigate time-dependent effects such as the coupling of power into the electrons and ions and the growth of the charged particle densities before, and immediately after, sheath formation. Results from the simulation have been extremely important in building general analytic models of the plasma behaviour (see "Simulation of plasma breakdown in a low pressure rf plasma" ).

The effect on multiple pulses on parameters such as the plasma density, currents, potentials and power coupled into the plasma have also been investigated (see "Pulsing a low pressure rf plasma" ). Pulsed plasmas are of increasing interest in materials processing applications, for improved film properties in deposition and increased uniformity for etching. They have also been used to reduce powder formation in chemical vapour deposition reactors. In order to understand and extend their application in commercial ventures it is essential to understand the physical processes taking place during pulsing.

Currently work is being done on including an "L-series" matching network in the simulation plasma model. The matching network is used in the experimental system to efficiently couple power from the generator into the plasma. In the process of doing so the network has a large influence on the current/voltage waveforms applied to the reactor electrode and hence on the behaviour of the plasma. In particular during breakdown the plasma impedances are changing rapidly, which consequently effects the power supplied to the plasma.In order to better understand how the matching network and the plasma interact, and to better model the experimental system, it was decided to explicitly include the matching network in a PIC simulation. Ultimately it is hoped that by better understanding the influence of the matching network on the plasma formation and growth, improvements to the circuit design can be made, in particular for pulsed systems in which the plasma experiences predominately non-equilibrium conditions.

Return to SP3 Home Page