Double ionization of helium by electron-impact: Complete pictures of the four-body break up dynamics

A. Dorn,¹ A. Kheifets,² C.D. Schröter,¹ C.Höhr,¹ G. Sakhelashvili,¹ R. Moshammer¹ and J. Ullrich ^1,3

¹ Universität Freiburg, Hermann-Herder-Str. 3, 79104 Freiburg, Germany

² Research School for Physical Sciences and Engineering, Australian National

University, Canberra, ACT 0200, Australia

³ Max-Planck-Institut für Kernphysik, Saupfercheckweg, Heidelberg, Germany

Abstract:

The dynamics of He double ionization by 2 keV electron-impact is studied experimentally for a momentum transfer of 0.6 a.u. at excess energies of 10 eV and 40 eV. Complete sets of fivefold differential cross sections are presented for all electron emission angles in coplanar geometry testing theory in unprecedented detail. Contributions beyond the 1^st Born approximation are identified comparing experimental data with first order convergent close-coupling (CCC) calculations which are in considerably better agreement with the present experiment than with the earlier measurement of Taouil et al. [Phys. Rev. Lett. 81, 4600 (1998)].

A full understanding of the correlated fragmentation dynamics of an atomic system upon impact of a charged particle or a photon is one of the central aims in atomic collision physics. While for the most basic three-body break up processes such as electron impact single ionization of hydrogen or photo-double ionization (PDI) of helium a rather profound understanding is emerging [1, 2], the transition to true many-body systems still remains a challenge, both experimentally and theoretically. With the availability of new experimental multi-coincidence techniques we now have the opportunity to obtain complete momentum space pictures of complex many-body processes such as double ionization of helium by electron impact, a so-called (e,3e) reaction leading to four unbound particles [3, 4].

On the theoretical side, fairly sophisticated models have been employed [5-7] to describe the first (e,3e) experiment on helium [8]. Because of a large disparity in the energies of the fast projectile (5.6 keV) and the slow ejected electrons (10 or 4.5 eV) it was natural to limit the projectile-target interaction to the first order while treating the interaction of the two slow ejected electrons nonperturbatively [5,6]. However, these first-Born calculations produced confusing results. Agreement with the experiment was poor, both in magnitude and in shape, especially at the lowest 4.5 eV ejected electron energy. Some of the experimental features such as strong peaks in the cross section for small relative electron emission angles could not be reproduced at all. Agreement with the experiment seemed to improve when a full four-body model was employed [7]. In the meantime, the authors of Ref. [6] did not rule out the possibility that some 'hidden' artefacts had actually effected the experiment. Therefore, the matter remains controversial and clarifying experimental and theoretical studies are highly desirable.

With the aim to resolve this controversy we present in this letter the data from a kinematically complete experiment for 2 keV electron impact on helium in which, for the first time, a large part of the 12-dimensional, 4-particle final-state momentum space is mapped with sufficient statistics to extract fully differential cross sections. Thus, theory can be tested for kinematics ranging from the optical limit to high momentum transfer up to 5 a.u. and over a large range of relative emission angles as well as energy partitions between the two slowly ejected electrons (E_b,c < 30 eV). Similarly to the previous experiments [6, 8] performed very close to the optical limit, we select here a relatively small momentum transfer of |q| = 0.6 a.u., equal energies of the ejected electrons of E_b = E_c = 5 eV and 20 eV and the coplanar geometry where the ejected electrons are emitted within the scattering plane of the projectile. We compare these data with calculations performed within the same first Born model as employed in [6]. The slow ejected electron interaction was treated nonperturbatively using the convergent close coupling (CCC) method. The method is known to yield very reliable quantitative results for the related PDI process when the two electrons are ejected from the helium atom by photon impact [9, 10].

The present experiment is performed applying a novel multi-electron – recoil-ion coincidence technique which has been demonstrated to enable (e,3e) experiments on helium [3]. Details of the working principle and the data analysis are described elswhere [4, 11]. In short, a supersonic jet provided a well localized (2 mm diameter) and dense (10¹¹ atoms/cm³) helium target at the intersection point with a pulsed electron beam. Ions and slow electrons produced in ionizing collisions are extracted to opposite directions by means of static electric and magnetic fields and detected by two position sensitive multichannel plate detectors. From the measured positions and times of flight the momentum vectors of two slow electrons k_b and k_c (E_b,c < 30 eV) and the momentum vector of the recoiling ion k_He⁺⁺ emitted in an (e,3e)-reaction are determined. The kinematics of the fast scattered electron as well as the momentum q transferred by the scattered projectile follows from momentum conservation

k₀-k_a = q = k_b + k_c + k_He⁺⁺. (1)

Here k₀ and k_a are the momenta of the incoming and the scattered projectile, respectively.

The electron detector is equipped with a fast delay-line readout and a multi-hit time-to-digital converter. Therefore, position as well as arrival time of the second electron emitted in a DI event is determined if the flight-time difference between two electrons exceeds 15 ns. Whereas the complete final-state momentum space is mapped for all ions with k_He⁺⁺ < 5 a.u., this detector dead-time results in a small loss of the total momentum space for the second electron hitting the detector.

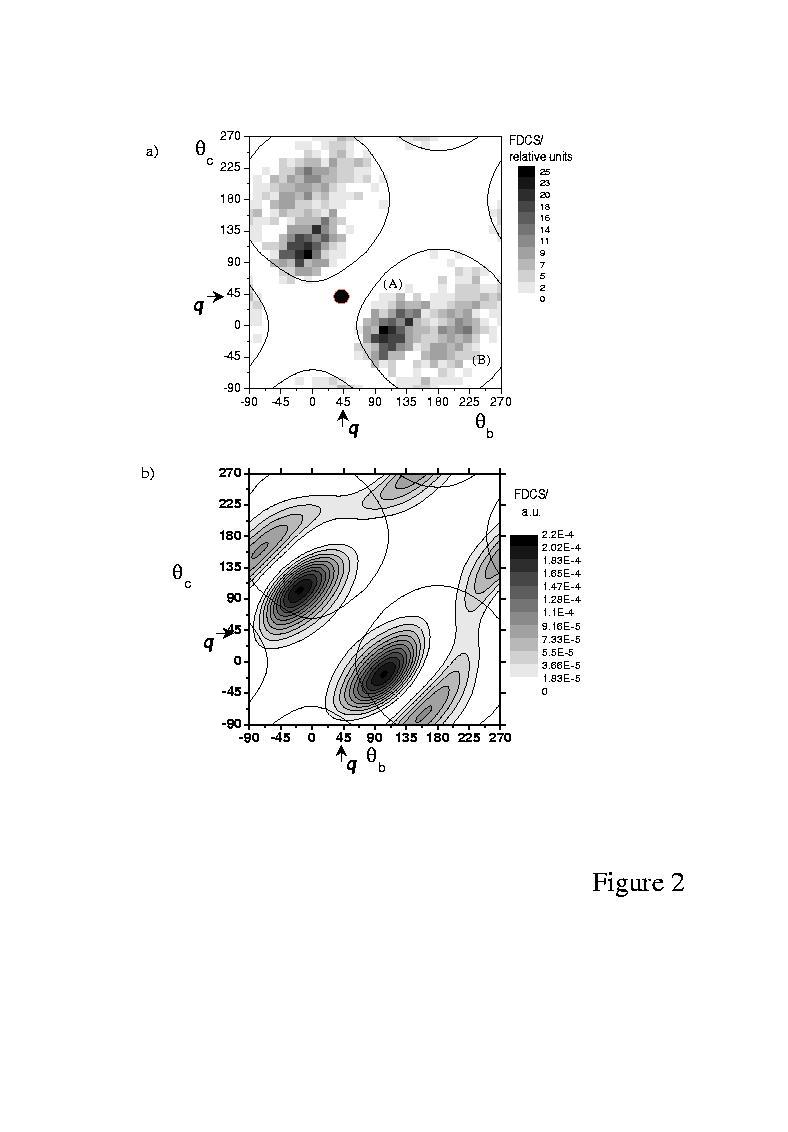
In figure 1 (a) the fivefold differential cross section (FDCS) is given as function of the ejected electrons emission angles q_b and q_c with respect to the forward projectile beam direction. The momentum transfer is |q| = 0.6 a.u. corresponding to the projectile scattering angle of q_a = 2.5° and the energies of the ejected electrons are E_b = E_c = 5 eV. We have chosen a density plot representation to visualize a large range of angles q_b and q_c being particularly well suited to study the overall structure of the cross section and to reveal symmetries as well as nodal lines. The angular range which is not affected by reduced detection efficiency due to the electron detectors dead-time is inside the circular solid lines in the diagrams.

The cross section pattern consists of a four peak structure. Both peaks in the upper left are equivalent to the peaks in the lower right of the diagram (marked A and B) since for symmetric energy sharing E_b = E_c both ejected electrons are interchangeable.

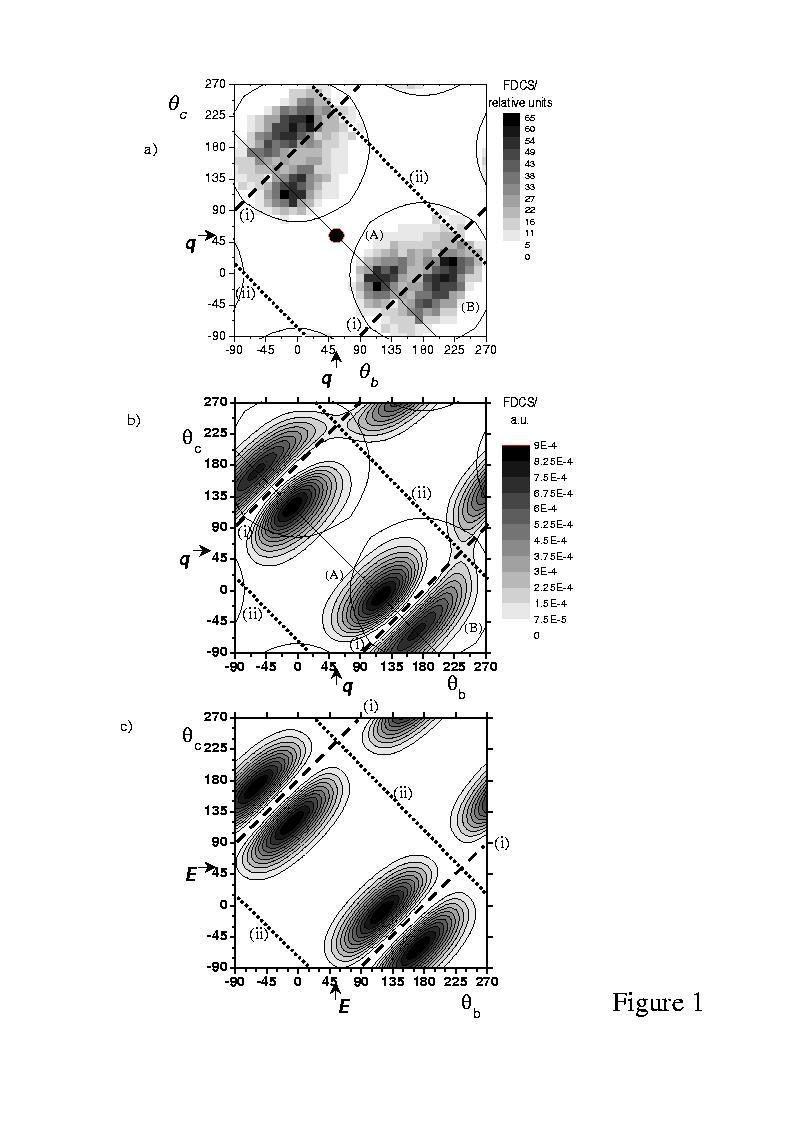
In Figure 1 we also present the theoretical CCC result (b) as well as the PDI cross sections (c) obtained by using the phenomenological parametrization of from Huetz et al. [12], which is commonly accepted to yield good agreement with experimental data. This parametrization nicely reveals the origin of the observed structures in factorizing the cross section in an angular part arising from photoabsorption and a correlation part describing the electron-electron repulsion in the final state [2]:

ds(k_b, k_c, E_b=E_c)=(cosq_bE + cosq_cE)²×C(b,c).

Here q_bE and q_cE are the emission angles relative to the electric field vector E. The angular factor mirrors the ¹P^O symmetry of the final state and hence it gives rise to zeros in the cross section arising from dipole selection rules: there is a first node (i) for back to back emission of both ejected electrons q_b - q_c = 180° (dashed lines in figure 1 a-c) and a second node (ii) if the sum momentum of the ejected electrons is perpendicular to the electric field vector (k_b+k_c) ^ E or equivalently q_bE + q_cE = 180° (dotted lines in figure 1). The correlation factor C(b,c) is zero for parallel emission, giving rise to the nodal line for q_b = q_c, and peaks for back to back emission of both electrons where their repulsion is a minimum. It can be very well approximated by a Gaussian function with the maximum centered at q_b - q_c = 180°, and a full-width at half-maximum which depends on the electrons’ energy. Since electron repulsion acts similarly for the (e,3e) process a large part of the experimentally non-accessible angular range, for emission of both electrons into the same direction q_b » q_c at equal energies, is not of a major importance as the cross section is close to zero in this region. A further property of the PDI cross section is the reflection symmetry with respect to a plane perpendicular to the electric field axis since both directions along the axis are equivalent and indistinguishable. Therefore the cross section shows reflection symmetry with respect to the lines (i) and (ii). Examining the experimental and theoretical (e,3e) cross sections, it immediately becomes obvious that both are governed by the same nodal lines showing close similarities to PDI despite the fairly large momentum transfer of |q| = 0.6 a.u.. This has been discussed before for conditions even closer to the optical limit by Lahmam-Bennani et al. [5]. On the other hand, distinct differences are observed which we will classify as being first due to non-dipole contributions and second due to higher order interactions with the projectile. First, contributions beyond the dipole approximation are result of momentum transfers |q| larger than the minimum transfer for photoabsorption |q_g| =E_g /c and, consequently, do not obey the dipole selection rules. As a result, the cross section in the CCC calculation is finite for back to back emission with one electron going into the momentum transfer direction, i.e. a configuration which is strictly forbidden by both dipole selection rules (i) and (ii). As a further consequence any q > q_g breaks the reflection symmetry of the cross section with respect to a plane perpendicular to the quantization axis since the direction along q now is distinguishable from the one opposite to q. Thus, in figure 1 a, b the cross section maximum (A) is stronger and less elongated compared to the maximum (B) for which both electrons enclose angles larger than 90° with q. These features become even more pronounced if the energies of the ejected electrons are higher. For E_b = E_c = 20 eV (figure 2 a, b) peak (A) becomes the dominant structure in the cross section which can be understood as follows: dipole transitions dominate in the transition matrix element not only in the limit of small momentum transfer where the transition operator reduces to the dipole operator but also if the energies of the ejected electrons are small. With decreasing energies E_b,c the low angular momentum terms in a partial wave expansion of the two-electron final state wavefunction dominate more and more for small distances from the ion, i.e. in the volume which largely determines the transition matrix element. Therefore, dipole transitions are emphazised for E_b,c= 5 eV despite the relatively large momentum transfer. For E_b,c= 20 eV peak (A) is dominant since for the corresponding emission angles so-called Bethe kinematics is closely fulfilled. Here the sum momentum of the ejected electrons is close to the momentum transfer k_b + k_c » q both in magnitude and direction, i.e. the ion momentum is small. This condition has been shown by Berakdar and Klar [13] to be the preferred collision kinematics for the (e,3e) process. Correspondingly to the nomenclature used for the (e,2e) cross sections, we name maximum (A) the “binary peak” and maximum (B) the “recoil peak” since for this maximum the electrons sum momentum is directed opposite q and the residual ion carries considerable momentum.

In all features discussed so far experiment and the CCC theory agree remarkably well. In the experimental data the nonzero cross section in between the cross section maxima (A) and (B) is consistent with the present resolution for the momentum transfer direction indicated by the size of the black circle in figures 1a and 2a. The remaining differences between experiment and CCC theory can be assigned to higher order projectile-target interactions. Any process of the first order reveals complete axial symmetry of the cross section with respect to the momentum transfer direction. Thus, the theoretical cross sections (figures 1b, 2b) must be invariant for inversion at the point indicating the momentum transfer direction or, equivalently, for reflection of both momentum vectors at the direction of q. The cross section peaks lie exactly on the straight solid line going through the point indicating the momentum transfer direction. While in the experimental data this symmetry is closely fulfilled for the binary peak (A), the recoil peak (B) shows a distinct shift to larger angles for both electrons. Therefore, higher order interactions are of importance and explain to the failure of first order theories for certain parts of the final state momentum space. Since the recoil peak (B) decreases strongly in magnitude for higher energies of the ejected electrons E_b,c becoming a relatively unimportant feature in figure 2, we can clearly prove experimentally previous assumptions made by Kheifets et al. [6] namely, that second order effects are more important for smaller energies E_b,c.

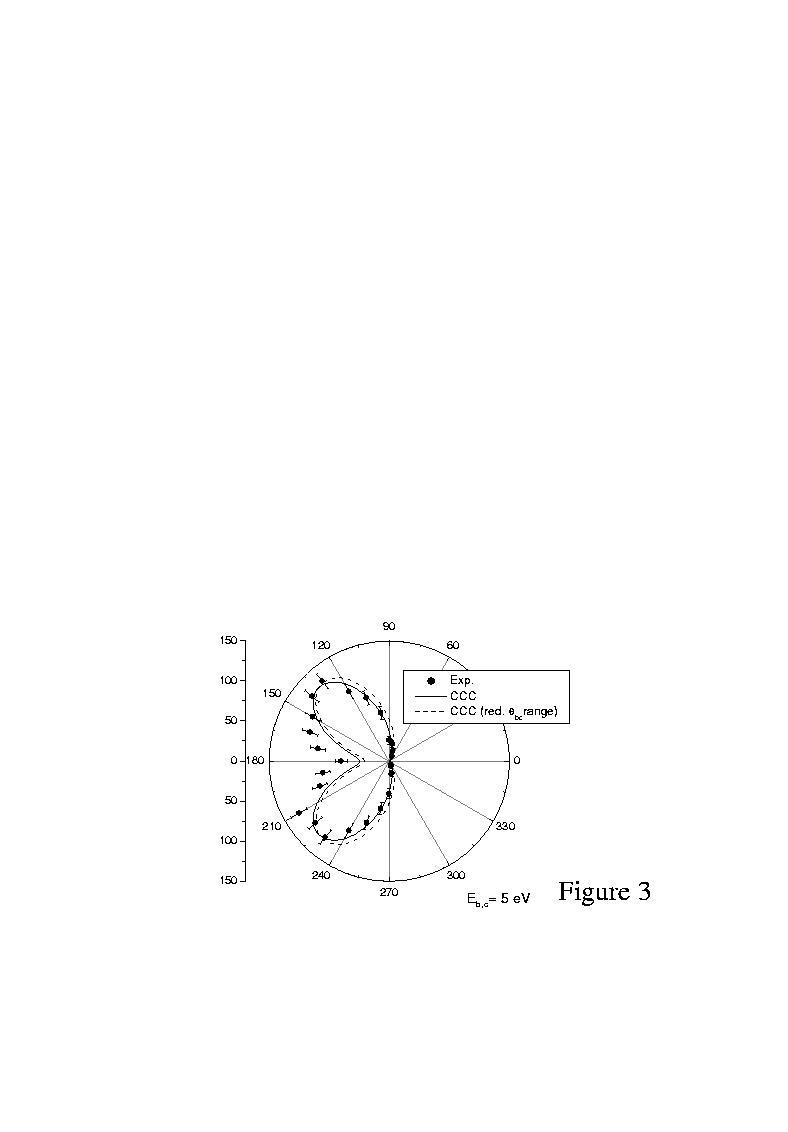
Finally, the cross section for E_b,c = 5 eV as function of the mutual angle q_bc= (q_b - q_c) integrated over the whole range of the individual angles q_b and q_c is presented in figure 3. The agreement with theory is quite satisfactory in particular if the reduced accessible angular range of the experiment is taken into account (full line in the figure). The width of the cross section minimum for small mutual angles is consistent with observations from PDI at similar excess energies: A fit of the PDI parametrization formula to the theoretical data results in full width half maximum (FWHM) of the Gaussian correlation factor of q_FWHM = 87° which is in good agreement with q_FWHM = 87° ± 2° reported for the PDI TDCS [14]. Thus, within the angular range accessible in the present experiment we cannot confirm somewhat surprising experimental observations from Kheifets et al. [6] who reported a four-lobe structure for E_b,c= 4 eV with two strong maxima at a small relative angle of q_bc = 60°. On the other hand we can confirm a filling of the node at q_bc = 180° which cannot be attributed to be only due to instrumental angular resolution but also indicates non-first Born processes.

In conclusion, the present experimental data allow for a large scale view of the final state momentum space and, therefore, enables the identification of general symmetries and structures of the cross section. In contrast to earlier studies, remarkably good agreement with the CCC calculations is found concerning all features in the shape of the cross sections which can be described within a first order approach, i.e. relative peak heights and widths as well as the position of nodal lines for both cases E_b,c= 5 eV and 20 eV. We also observe a break of symmetry of the cross section with respect to the momentum transfer direction which is a clear signature of higher order interactions which are not included in theory. For the partially integrated cross section as function of the mutual angle q_bc good agreement is obtained which is in contrast to recent experiments closer to the optical limit.

Acknowledgments: Support from the Deutsche Forschungsgemeinschaft within the SFB 276, project B7 and within the Leibniz programme is gratefully acknowledged.

References:

1. Rescigno T. N. , Baertschy M. , Isaacs W. A. , and McCurdy C. W. , Science 286, 2474 (1999)

2. J. S. Briggs and V. Schmidt, J. Phys. B 33, R1 (2000)

3. A. Dorn, R. Moshammer, C.D. Schröter, T.J.M. Zouros, W. Schmitt, H. Kollmus, R. Mann and J. Ullrich, Phys. Rev. Lett. 82, 2496 (1999)

4. R. Moshammer et al., Nucl. Inst. Meth. Phys. B 108, 425 (1996); H. Kollmus et al., Nucl. Inst. Meth. B 124, 377 (1997)

5. A. Lahmam-Bennani, I. Taouil, A. Duguet, M. Lecas, L. Avaldi, and J. Berakdar. Phys. Rev. A, 59, 3548 (1999)

6. A. Kheifets, I. Bray, A. Lahmam-Bennani, A. Dueguet, and I. Taouil, J. Phys. B 32, 5047 (1999)

7. J. Berakdar, Phys. Rev. Lett. 85(19) (2000)

8. I. Taouil, A. Lahmam-Bennani, A. Duguet, M. Lecas and L. Avaldi, Phys. Rev. Lett. 81, 4600 (1998)

9. A.S. Kheifets and I. Bray, J. Phys. B 31, 5149 (1998)

10. A. S. Kheifets and I. Bray, Phys.Rev.Lett 81, 4588 (1998)

11. J. Ullrich et al., J. Phys. B 30, 2917 (1997)

12. A. Huetz, P. Selles, D. Waymel and J. Mazeau, J. Phys. B 24, 1917 (1991)

13. Berakdar J and Klar H., J. Phys. B 26, 4219 (1993)

14. O. Schwarzkopf, B. Krässig, J. Elmiger, and V. Schmidt, Phys. Rev. Lett. 70, 3008 (1993)

Figure 1: Fivefold differential cross section (FDCS) in coplanar scattering geometry as function of the ejected electrons emission angles q_b and q_c relative to the primary beam forward direction. a) Experimental cross section for E₀ = 2 keV, |q| = 0.6 ± 0.2 a.u. and E_b = E_c = 5 ± 2.5 eV. The direction of the momentum transfer q is marked by arrows and the black dot in the diagram; it’s size indicates the uncertainty in the direction of q resulting from the finite integration interval of |q|. The angular range which is not affected by the detector dead-time is encircled by solid lines. b) CCC calculation for E_b = E_c = 5 eV. c) FDCS for photo-double ionization with E_b = E_c = 5 eV obtained with the parametrization of Huetz et al.(see text). The electric field vector E has been oriented to coincide with the corresponding quantization axis q for the (e,3e) process in figure (a) (q_E = q_q » 55°).

Figure 2: As for figure 1 except E_b = E_c= 20 ± 4 eV. a) experimental FDCS. b) CCC calculation.

Figure 3: Cross section as function of the mutual angle q_bc= (q_b - q_c) integrated over all values of the individual q_b and q_c for E_b = E_c = 5 eV. The CCC calculation for the full angular range and for the angular range accessible experimentally is given as dashed line and continuous line, respectively.