COMPLETE EXPERIMENTS FOR THE DOUBLE IONISATION OF He:

(e,3e) CROSS SECTIONS AT 1keV IMPACT ENERGY

AND SMALL MOMENTUM TRANSFER

A. Lahmam-Bennani^(a,b), A. Duguet^(a), M. N. Gaboriaud^(a), I. Taouil ^(a), M. Lecas,^(a)

A. Kheifets^(c), J. Berakdar^(d) and C. Dal Cappello^(e)

^(a)Laboratoire des Collisions Atomiques et Moléculaires (UMR 8625)

Bât. 351, Université de Paris-Sud XI, F-91405 Orsay Cedex, France

^(c)Research School of Physical Sciences, The Australian National University,

Canberra ACT 0200, Australia

^(d)Max-Planck Institut für Mikrostruktur Physik, Weinberg 2, D-06120 Halle, Germany

^(e) Institut de Physique, LPMC, 1 Boulevard Arago, Technopôle 2000, F-57078 Metz, France

^(b) Author to whom all correspondance should be addressed

e-mail : azzedine@lcam.u-psud.fr

Physics Abstracts Classification : 3450H, 3480D

Short Title : (e,3e) cross sections for He at 1 keV

submitted to J.Phys.B : At.Mol.Opt.Phys., January 25, 2001

Abstract

The relative, coplanar angular distributions of electrons, produced in an electron-impact double ionization of helium (e,3e reaction), have been measured at 1.1 keV impact energy. The momentum transfer was 0.45 a.u. and the two "ejected" electrons were detected with the same energy of 10 eV. The general features of the angular distributions are discussed. The data are analysed in different angular modes which allows a detailed comparison with state-of the art calculations. For high incident energy and small momentum transfer, as in the present case, the (e,3e) cross section can be related to the single -photon double ionisation (PDI). We exploit this fact and compare the present findings with the PDI and identify the contribution of non-dipole effects.

1. Introduction

The study of atomic electron-impact double ionisation, also called the (e,3e) reaction, provides a powerful and straightforward tool to investigate the dynamics of interacting, highly excited few-electron systems (three highly excited electrons in the field of a residual ion). A rather complete picture of the (e,3e) process is obtained by performing an experiment in which the momentum vectors of all the particles are determined (a complete experiment would require resolving the spins as well). In the present experiment the reaction cross section is measured while the solid emission angles of the three electrons and the energies of two of them are determined, i.e. a five-fold differential cross sections (5DCS) is registered. Other kinematical variables of the involved particles are obtained from the energy and (linear) momentum conservation laws.

Recently, we conducted a systematic study of the (e,3e) reaction employing various targets (Kr [1], Ar [2], Ne [3] and He [4-6]). Basically, all these measurements haven been carried out at a relatively high impact energy ( ~5.5 keV) and a small momentum transfer to the target. Therefore, the corresponding theoretical models [5-10] have been designed in the spirit of the first Born approximation (FBA) for the projectile-target interaction. Most of the theoretical results have been obtained using He as a target since the residual ion (the alpha particle) has no relevant internal structure leading thus to a simplified theoretical treatment. The comparison of these theories with the experiments have lead to the following observations. The absolute magnitude of the calculated cross sections was largely different from one calculation to another and from the experimental absolute data. In general, however, the qualitative features of the measured angular correlation patterns at various fixed ejection angles were reproduced by the theories. In several cases the calculations deviated significantly from the experiments with regards to the shape of the angular correlation patterns. This disagreement was attributed, at least partly, to the non-first Born effects which were not included in most of the theoretical models (note that the C4FS model described in [5] went somehow beyond the FBA). Similar effects have also been observed in Ar [2] and, to some extent, in Ne [3]. In addition, it was found that the dipole limit was approached differently at various electrons ejection angles despite the fact that the amount of momentum transferred from the projectile to the target remained constant. This means that in the case of double ionisation the optical limit depends not only on the incident energy and the amount of momentum transfer, as is the case for single ionisation, but it also depends on the emission direction of the slow ejected electrons, see [11]. These deviations are seen to be energy dependent and are expected to become larger at lower incident energy in which case the optical limit is increasingly violated. We have therefore performed new low impact-energy experiments ( ~1 keV) in a similar scattering geometry to the work reported in [5] at 5.5 keV. The goal is to address the origin of the deviations between the experiments and FBA type calculations. To this end, our data will be compared to results from three standard theoretical models, which have been shown to be successful for the description of single ionisation processes or photo double ionisation processes. Two of these models utilise the FBA in a sense described above. This approximation reduces the four-body problem (three electrons in the field of residual ion) to a three-body one (the two slow electrons in the residual-ion field). The latter problem is then approached within the framework of the three Coulomb wave method (3C) [12] or using the convergent close coupling (CCC) formalism [13]. Alternatively, the third model employes a correlated four-body final state (C4FS) as described in [5] and references therein and goes beyond the FBA via the introduction of effective charges. However, as noted in [6], the variation of the effective charges is small, and the non-first Born effects due to this model should be weak.

Throughout this paper, the same notations as in [5] are used. In particular, positive scattering and ejection angles are counted counter-clockwise, starting at the incident beam direction.

2. Experimental

2.1 Experimental procedure

The experimental set-up and procedure have been described extensively elsewhere [2, 6, 14]. Briefly, a coplanar arrangement is used where the incident and the three outgoing electrons lie in the same plane. The impact energy is E₀ = 1099 eV. The scattered electron is observed at a fixed angle, q_a= +1.10°, with an energy E_a = 1000 eV (corresponding to a fixed momentum transfer, K = 0.45 au, in the direction q_K = - 21.6°). The value of the scattering angle is measured with an accuracy of ± 0.02°, whereas the spectrometer acceptance angle is Dq_a = ± 0.10°, which corresponds to a high momentum transfer resolution DK < ± 0.006 au, and a small uncertainty in the momentum transfer direction, < ± 0.9°. The two ejected electrons have identical energies, E_b = E_c = 10 eV. They are selected in two opposite half planes with respect to the electron beam in a double toroidal electrostatic analyser. The angular information contained in the collision plane (k₀, k_a), i.e. the ejection angles q_b and q_c, is preserved upon arrival on the position sensitive detectors. Therefore, multi-angle collection of the ejected electrons is realized over the useful angular ranges 20° < q_b <160° and 200° < q_c < 340°. The energy and angle resolutions for the ejected electrons are fixed in the off-line analysis [14] to DE_b = DE_c = ± 2 eV, and Dq_b = Dq_c = ± 8°. As far as the present paper is concerned, the data have been sorted into three modes: (i) the so-called 'fixed ejected angle mode' where the escape direction q_b or q_c of one electron is fixed and the other one is mapped on to the opposite half-plane, (ii) the 'fixed mutual angle mode’ at fixed q_bc = (k_b, k_c) but varying q_b or q_c, and (iii) 'the symmetric geometry mode' where both electrons emerge with equal but opposite angle with respect to the incident beam, q_b = - q_c. A fourth mode, the so-called 'summed mutual angle mode' with varying q_bc but summing over all individual directions q_b or q_c which lead to the same q_bc has been discussed in [11] and will not be repeated here.

The long accumulation time needed to achieve a reasonable statistical error (~ 32 days of continuous, non-stop acquisition for all the data presented in this paper) resulted in a fatigue effect on the detectors, which was corrected as explained in [2, 3, 6, 14] by daily recording 'reference' (e,2e) distributions. These distributions were also used as an angular calibration of the toroidal analysers by comparing the measured (e,2e) spectra with well-established theoretical ones such as the orthogonalized Coulomb wave (OCW) calculations or the convergent close coupling (CCC) calculations. After these corrections (which amount to less than 10 - 15%), all the angular distributions presented in this paper are obtained on the same relative scale. In this work, main emphasis is put on the accurate determination of the shape of the distributions to be compared with the different theoretical models. Therefore, no attempt was made to determine the absolute scale for the measured cross sections.

Finally, it should be emphasised that, as discussed in [6], the finite angular and energy resolutions used in this work are not expected to have a severe effect on the measured (e,2e) or (e,3e) distributions since it is unlikely that these distributions will have to exhibit any sharp structures.

2.2 Results

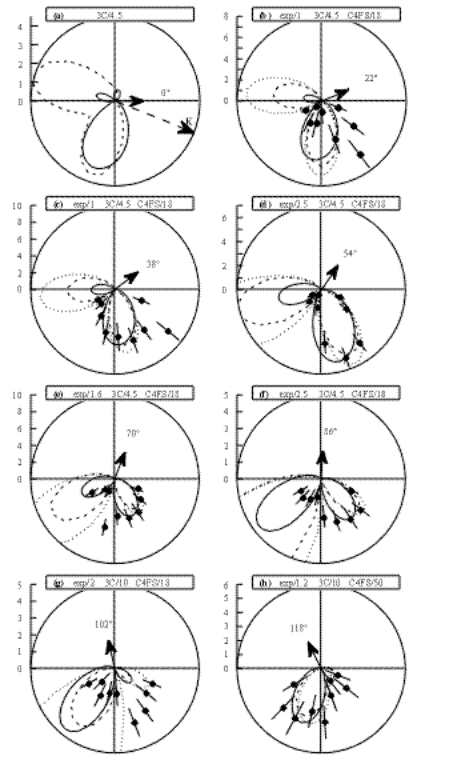
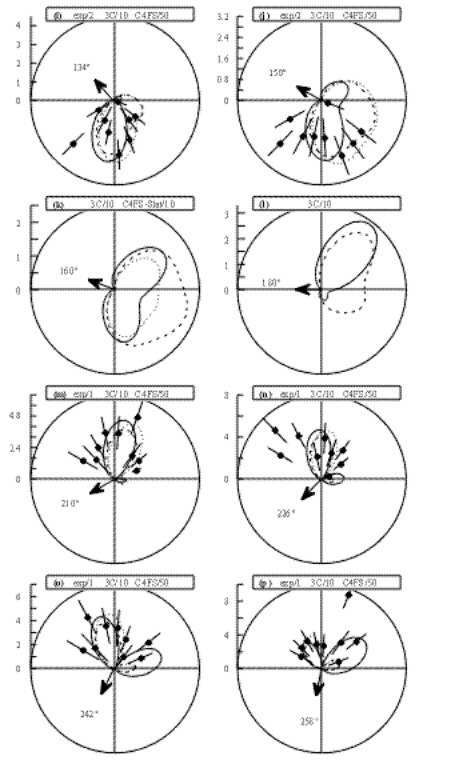
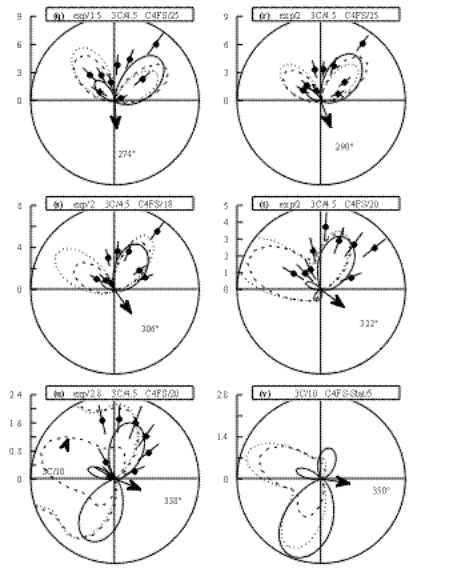
The calculated and measured 5DCS are shown in figure 1 (a) to (v) and in figure 2 (a) to (f) according to the 'fixed ejected angle mode', that is as angular distributions of one electron for fixed emission direction of the second one. In these plots and in the following discussion, we denote by q_fix and q_var the fixed and the variable electron angles, respectively. Figure 3 (a) to (c) corresponds to the so-called 'fixed mutual angle mode', that is with variable q_b and q_c angles while keeping the mutual angle q_cb fixed. Finally, figure 4 presents the so-called symmetric geometry where both electrons emerge at equal angles on both sides of the incident beam, q_b = - q_c. The fast electron is observed at an angle q_a = +1.10°, not shown in the figures, hence the +K direction at q_K = -21.6° as indicated in Fig. 1(a).

Since the data are only relative, we arbitrarily choose to plot all the results by renormalising them to the absolute scale given by the CCC results. In doing so, and for the sake of clarity of the figures, we have used different scaling factors between experiment and CCC. Similarly, though the 3C and the C4FS results are of course absolute, we have chosen to plot them after a rough renormalisation to the CCC ones, as indicated in the figures, in order to put the emphasis on the shape comparison. (This choice is arbitrary and is not meant to favour one model over the others). However, we recall that the experimental data are obtained on the same relative scale. Therefore, the internal change in the scaling factor between the experiment and each theoretical model is a measure of the ability (or unability) of this model to reproduce the relative scale of the data, whereas its variation from one model to another is a measure of the consistency of the theoretical models to reproduce the absolute scale.

2.2 1. Fixed ejected angle mode

As a first observation from figure 1, one may compare between the three theoretical results. They generally all yield a two lobes structure for the 5DCS angular distributions. The two lobes are separated on the one hand by a strict zero intensity for the parallel emission (see however the discussion below of figure 3 (c)), due to the Coulomb repulsion between two electrons with equal energies emerging in the same direction, and on the other hand by a deep minimum of intensity for the anti-parallel or back-to-back emission. This minimum is reminiscent of the node observed in photo double ionisation (PDI) where the back-to-back emission is forbidden, due to the electron pair final state symmetry [15]. The origin of the dips and maxima in the (e,3e) cross section and the connection to their PDI counterparts have been explored in Ref. [5].

Noticeable exceptions to the two lobes structure are:

(a) on the one hand, cases (a), (t), (u) and (v) corresponding to the fixed electron being emitted forward with respect to the momentum transfer vector, K. Here, a third intensity maximum appears roughly in the direction opposite to the fixed electron direction. This maximum appears as a distinct, small lobe in the CCC results and a much wider structure in the 3C and C4FS results. As the back-to-back emission of the two photoelectrons is forbidden in PDI process, the finite (e,3e) intensity in this back-to-back configuration must be attributed to non dipolar contributions. As discussed in [16], within the FBA, only even-parity multipoles of the Born operator contribute to the back-to-back emission. To see this directly we write the (e,3e) transition amplitude in the form:

T_(e,3e) µ <Y_kb,kc(r_b, r_c) | cos(K.r_b) + cos(K.r_c) | F(r_b, r_c) > +

i <Y_kb,kc(r_b, r_c) | sin(K.r_b) + sin(K.r_c) | F(r_b, r_c) > , (1)

where Y_kb,kc(r_b, r_c) and F(r_b, r_c) are the wave functions of the two slow electrons in the final and initial state, respectively. In general, the final-state wave function does not possess a defined parity. However, in the case k_c = - k_b (i.e., in the back-to-back configuation) Y_kb,kc(r_b, r_c) has an even parity. This follows directly and in an exact manner from the structure of the Schrödinger equation that dictates:

Y_kb,kc(r_b, r_c) = [ Y_kb,kc(r_b, r_c) + Y_-kb,-kc(-r_b, -r_c) ] .

Therefore, only the cosine term in the expression (1) for T_(e,3e) contributes in the back-to-back emission case.

(b) Cases (j), (k), (l) and to some extent case (i) corresponding to the fixed electron being emitted backward with respect to the K vector. Here, a strong filling of the minimum corresponding to the back-to-back emission is observed, though less strong in the CCC than in the C4FS results. This is again a clear evidence of non-dipolar contributions which even dominate the dipole term. Or more precisely, as discussed above, the filling of the back-to back emission node in PDI is due to first term in Eq.(1), i.e. to the odd part of the transition operator. The three theoretical models shown here do not predict the same relative importance for these non-dipole terms. Such effects are appreciably larger than those reported at 5.5 keV impact energy in [6] and [11], as it is expected due to the lower incident energy and to the larger momentum transfer employed in the present work.

(g) apart from these cases where the fixed electron is observed backward or forward in the vicinity of the incident beam direction, the three theories predict a small probability for the back-to-back emission in agreement with the PDI expectation, meaning that the optical limit is here closely approached. All observation (a)-(g) confirm the conclusion made in [5] and [11] that the dipolar limit is reached differently depending on the directions of the momentum vectors k_b and k_c, even though the momentum transfer, the incident energy and the outgoing electrons’ energies are kept fixed.

Now let us have a closer look at the shape of the theoretical distributions in Fig. 1. The intensity ratio of the two lobes, when present, is quite different from one model to another. For instance, CCC calculations predict one large and one small lobe in case (b) where q_fix = 22°, while both C4FS and 3C calculations yield two almost identical lobes. The situation is practically reversed in case (o) where q_fix = 242°, with two identical lobes for CCC and very asymmetric lobes for C4FS and 3C. Generally speaking, the distributions obtained with the C4FS and 3C models are very close to each other as to the shape, and are significantly different from the CCC ones. This can be explained by the way the final state wave function is calculated in different models. The C4FS and 3C final state wave functions are most accurate at the asymptotic region of large distances from the nucleus. On the contrary, the CCC final state wave function is accurate at a short range from the nucleus and looses its accuracy in the asymptotic region. Nevertheless, the CCC calculations with the same final state wave function provide reliable absolute cross sections for the related PDI process. In addition, the prediction of the CCC model agrees as to the shape with recent (e,3e) measurements obtained on a relative scale by Dorn et al [17] for a similar kinematics of a large incident energy and a small momentum transfer.

Another observation concerns the relative magnitude of the cross sections given by the three models. With the normalisation procedure explained above, one sees that there is a factor of 10 difference in magnitude between CCC and 3C results in cases (g) to (p), 3C yielding larger cross sections. This factor reduces to 4.5 in the other cases. We note that cases (g) to (p) correspond to the fixed electron being observed in the 'backward half plane' (with respect to the incident direction), that is 90° < q_fix < 270°, while the other cases correspond to the fixed electron being observed in the 'forward half plane' , that is -90° < q_fix < 90°. Similarly, the C4FS results are a factor of 10 to 50 larger than the CCC ones depending on the q_fix value, with more or less the same remark applying as to the backward and forward half planes. On the other hand, the ratio of 3C to C4FS results is almost constant, C4FS yielding about ~ 5 times larger cross sections at practically all q_fix values. Therefore, as noted above for what concerns the shapes, the C4FS and 3C models yield comparable results but both deviate significantly from the CCC calculations. Part of these deviations may have their origin in the following observation: the C4FS results presented here make use of a three-term Hylleraas type ground state description of the He atom. Calculations within the same model have also been performed using a poorer description of the initial state, namely a Slater type wavefunction. The results (not presented here) are very similar in shape to the Hylleraas ones, but differ in magnitude being a factor ~6 larger, the use of a yet another choice of initial-state wave function leads basically to the same shape of the angular patterns but alters significantly the absolute value of the cross sections. This may be taken as a good illustration of the sensitivity of the C4FS results to the initial state description. The 3C calculations utilize a six-term Hylleraas [18] type ground state wavefunction which gives a good value for the energy of the ground state (E = -2.903115 a.u.). The CCC calculations are performed with the more elaborate 20-term Hylleraas wavefunction. CCC calculations in the velocity gauge of the Born operator, not shown here, have also been performed with an 18-term MCHF expansion. They yield very similar results, proving the stability of the CCC calculation to the ground state wave function when a large basis set is used. Therefore, it is likely that at least part of the difference in absolute scale between the three theories has its origin in the quality of the ground state wavefunction. However, a clear-cut answer to this point would necessitate a direct comparison of several initial state wave functions of different quality using the same final state description, that is for each of the three theortical models.

In general, all three models do grossly reproduce the shape of the experimental 5DCS distributions of Fig. (1) within the uncertainty given by the error bars of the experiments and by the fact that the data are only recorded in one half plane. Nonetheless, there are obvious substantial deviations between theories and experiment:

(i) First, none of the considered models does correctly reproduce the relative scale of the experimental data. In addition, there is also no internal consistency in the relative scale between the different theoretical results. If cases (b) and (c) are taken as a reference where the normalisation constant between experiment and each theory is arbitrarily given a value equal to 1, then it can easily be inferred from Fig. 1 that it would be necessary to divide the experiment by a variable factor which takes values between 0.35 and 2.8 in order to bring the measured data in cases (d) - (u) in reasonable agreement with the calculated results. From the numerous tests performed, in particular by measuring known (e,2e) angular distributions, it is extremely unlikely that such a variable factor might be due to an experimental fault.

(ii) In a number of cases, e.g. (d), (h) and (o), the angular position of the calculated lobes is in a nice agreement with the measured ones, whereas for several other cases, e.g. (b), (g), (n) and (q) large shifts are observed, which may amount up to some 45°. In this respect, the C4FS and 3C models yield identical positions of the lobes, whereas the main lobe in the CCC model generally appears to be rotated backwards by ~ 10° with respect to the other models.

(iii) cases (u) and (k) are of particular interest since the fixed electron is observed along +K or (approximately) along -K, respectively. Under these conditions, it was shown [19] that any first order model must yield a symmetrical distribution about ±K. This is the case for all three models, including the C4FS which goes beyond FBA through the introduction of effective charges. This either means that the non-first order effects are intrinsically small under these geometries, or, as previously noted in [6] and [8] that their contribution to the C4FS cross sections is small. Unfortunately, the limited range of the experimental data does not allow concluding about a possible breaking of symmetry. It is also interesting to note that the three models predict a strong (CCC) or very strong (C4FS and 3C) relative contribution of the back-to-back emission under this geometry (this contribution is in fact maximum there, see figure 3 (a)). This appears to be in conflict with the experimental observation in case (u) where the measured back-to-back intensity approaches zero.

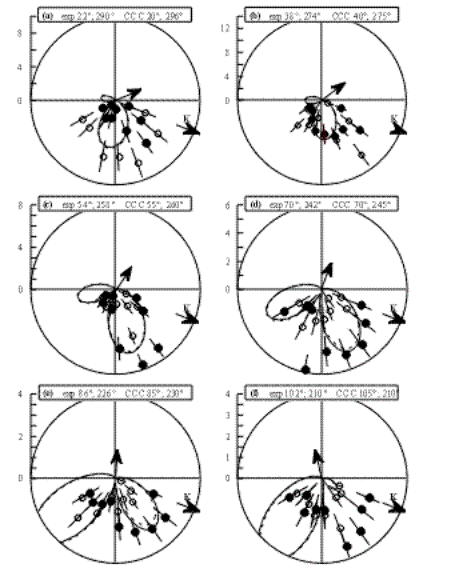
(iv) As noted in [6] and [11], the PDI cross sections distributions obtained for two electrons fixed angles which are symmetrical with respect to the electric field direction e must be mirror images of each other with respect to this e direction. In the electron impact case, K plays the role of e direction in the dipole limit. Therefore, we exploit this mirror symmetry in figure 2 in which some of the data of figure 1 are accordingly superimposed on each other. Comparison is made with the CCC results obtained under the same transformation. We see clearly from figure 2 that this symmetry transformation does not produce much change in the CCC results which are thus quite close to the dipole limit. On the other hand, even considering the large error bars, the experimental data are not invariant under such transformation. This might show how important are the deviations from the optical limit, but it might also indicate the large role played by non-first Born processes, even though the incident energy is large (1.1 keV) and the momentum transfer is small (0.45 au). A similar observation was made in [6], but in general the deviations from 'perfect' symmetry were smaller, as one would expect from the higher incident energy (5.5 keV) and smaller momentum transfer (0.24 au) used in [6].

2.2.2. Fixed mutual angle mode

Figure 3 presents angular distributions in the so-called fixed mutual angle mode, that is with variable q_b and q_c angles while keeping the mutual angle q_bc fixed. The experiments are compared to the CCC and the 3C results (C4FS results are almost identical to the 3C ones except for the magnitude). In Fig. 3 (a) and (b) the two ejected electrons emerge at large angle from each other, whereas in Fig. 3 (c) they asymptotically fly out close to each other which enhances the final state Coulomb repulsion between them. In all cases the two models do not produce the same magnitude of the cross sections as discussed above, hence different normalisation factors are used (as indicated on the figures) in order to put the emphasis on the shape comparison.

- Case (a) with a mutual angle q_bc = p is a very interesting one since it corresponds to the forbidden back-to-back emission in PDI (i.e., in PDI this graph would be a strict zero everywhere). In other words, this graph represents a direct measure of the non dipolar effects involved in the present (e,3e) process, in the sense discussed following Eq.(1). As noted above, theories predict these non dipolar effects to be maximum when the pair of electrons is ejected along ±K, whereas the maximum probability in the experiments occurs when the electron-pair axis is rotated by ~60° from this direction. Moreover, the two first order theories show the expected symmetry about ±K direction (at 338° and 158°, respectively) whereas the experiment does not. Both these angular shift and breaking of symmetry may be directly attributed to second or higher order effects in the projectile-target interaction process.

- In Fig. 3 (b) the data are too scarce to come to a definite conclusion. However, the data seem to indicate a minimum where the calculations show a maximum.

- In fig. 3 (c), though no data could be measured, it is interesting to compare the result of the two calculations. At 40° mutual angle both models yield almost undistinguishable angular distributions as to the shape. However, in contrast with all the above observations, the CCC cross sections are now a factor of 4 larger than the 3C ones. This might find its explanation in the 0° behaviour of the CCC. Indeed, at 0° mutual angle the 3C model (and the C4FS model) yield a vanishing cross section as expected from the Coulomb repulsion which forbids the two ejected electrons to emerge in the same direction with the same velocity. In contrast, CCC model fails to strictly fulfill this selection rule as it predicts a non-zero intensity. However, the corresponding cross sections are small, about two orders of magnitude smaller than a typical CCC lobe intensity in figure 1, and roughly one order of magnitude smaller than the "DPI-forbidden" intensities involved in Fig. 3 (a).

2.2.3. Symmetric geometry

In figure 4, the data have been sorted for the two ejected electrons to emerge at equal but opposite angles, q_b = - q_c. In (e,2e) processes, such symmetric geometry is well known to be very sensitive at large angles to second order effects [20], and has allowed to identify the observed (e,2e) large angle peak [21, 22] as being due to a double mechanism involving a backward elastic scattering of the projectile followed by a binary e -e collision. In this representation, the present theoretical and experimental results show two peaks, one forward at about 60° and one backward at ~ 130° in the experiment and ~110° in the theories. The experiment shows a backward to forward peak ratio of ~ 0.5. The CCC ratio of ~ 0.8 is close to the measurements, whereas the other two theories show ratios larger than 1, roughly 1.5. In the lower panel of the figure is plotted the corresponding magnitude of the ion recoil momentum, k_ion. Comparing the upper and the lower panels of the figure, a striking similarity is observed as to the position of the minimum (especially with the theoretical minimum) at q_b ~ 80°. When k_ion is minimum, the Bethe sphere is closely approached (the Bethe sphere is reached when the momentum transfer K is fully absorbed by the pair of ejected electrons, the ion remaining spectator, i.e. k_ion = 0). It has been argued [16] that under these kinematical conditions the cross section should be maximal, while it is observed here to be minimal. This apparent contradiction was also noted in [5] and was attributed to the fact that under the present near-dipole conditions, the optical transition is forbidden for two 'free' electrons which is the condition for the Bethe sphere. The fact that the experimental minimum occurs at a larger angle than in the calculations might be due to the non-dipole contributions which are not fully taken into account in the models as suggested above, e.g. in Fig. 3 (a).

3. Conclusion

We presented a large body of new experimental data on the (e,3e) fully resolved cross sections for the double ionization of helium, in the coplanar geometry and under equal energy sharing 10 + 10 eV. The data were compared in different angular modes with the best available first-order theories, namely the 3C, C4FS and CCC models.

The three theories do not predict the same absolute scale for the 5DCS. This could partly be due to the different descriptions of the initial state used, from poor to more elaborate. But, when compared to the experiments, they do not predict the correct relative scale for different angular distributions neither.

The experiments as well as all theories display a strong filling of the node corresponding to the forbidden back-to-back emission in PDI, or even display an additional lobe at this position. This behaviour obviously reflects a strong manifestation of non-dipolar effects in the projectile-target interaction which become prominent when the fixed electron is emitted either forward or backward around the momentum transfer direction . However, the three theoretical models do not predict the same relative importance for these effects. Such effects are appreciably larger than observed at 5.5 keV, as it is expected from the lower impact energy and larger momentum transfer of this work. Moreover, these effects do appreciably vary with the emission directions, which confirms our earlier conclusion [5,11] that the dipolar limit is reached differently depending on the orientation of the k_b and k_c vectors, even though the momentum transfer, the incident energy and the outgoing energies are kept fixed. A similar experiment at much higher incident energy, 10 keV or more, is highly desirable in order to probe when and how the optical limit is reached.

On the other hand, while the CCC theory almost fulfils the 'mirror symmetry' when superimposing angular distributions taken at symmetrical q_fix angles with respect to K, the experiments do not. This might indicate the large role played by non-first Born processes. Another indication for the importance of these effects is found when the pair of electrons is detected back-to-back while rotating the e - e axis (figure 3) : the three first order theories show the expected symmetry about ±K direction, whereas this symmetry is broken in the experimental data. A similar experiment at lower incident energy is also desirable in order to enhance the observed effects. Such experiment has been recently performed in our group and is currently under analysis.

Acknowledgments

The authors are grateful to Dr A. Huetz for helpful discussions. They also acknowledge the technical assistance and skills of Mr A. Abadia. One of the authors (AK) wishes to thank the Université de Paris-Sud XI for a Professeur invité position.

References

[1] Lahmam-Bennani A, Duguet A, Grisogono A M and Lecas M 1992 J. Phys. B : At. Mol. Phys. 25 2873

[2] El Marji B, Schröter C, Duguet A, Lahmam-Bennani A, Lecas M and Spielberger L 1997 J. Phys. B : At. Mol. Opt. Phys. 30 3677

[3] Schröter C, El Marji B, Lahmam-Bennani A, Duguet A, Lecas M and Spielberger L 1998 J. Phys. B : At. Mol. Opt. Phys. 31 131

[4] Taouil I, Lahmam-Bennani A, Duguet A and Avaldi L 1998Phys Rev Lett 81 4600

[5] Lahmam-Bennani A, Taouil I, Duguet A, Lecas M, Avaldi L and Berakdar J 1999Phys Rev A 59 3548

[6] Kheifets A, Bray I, Lahmam-Bennani A, Duguet A and Taouil I 1998 J. Phys. B : At. Mol. Opt. Phys. 32 5047

[7] El Mkhanter R and Dal Cappello C 1998 J. Phys.B : At. Mol. Opt. Phys. 31 301

[8] Grin M, Dal Cappello C, El Mkhanter R and Rasch J 2000 J. Phys.B : At. Mol. Opt. Phys. 33 131

[9] Nebdi H 2000 PhD Thesis Université Catholique de Louvain

[10] Popov Yu V, Dal Cappello C and Ancarani L U 2000 in Many Particle Spectroscopy of Atoms and Molecules, Clusters and Surfaces ed. by J. Berakdar and J. Kirschner, Plenum/Kluwer Press (2001).

[11] Lahmam-Bennani A, Duguet A, Taouil I and Gaboriaud M. N. in Many Particle Spectroscopy of Atoms and Molecules, Clusters and Surfaces ed. by J. Berakdar and J. Kirschner, Plenum/Kluwer Press (2001)

[12] Joulakian B, Dal Cappello C and Brauner M 1992 J. Phys B: At. Mol.Opt.Phys. 25 2863-2871

[13] Kheifets A S and Bray I 1998Phys Rev A 58 4501

[14] Duguet A, Lahmam-Bennani A, Lecas M and El Marji B 1998 Rev Sci Instrum 69 3524

[15] Huetz A, Selles P, Waymel D, and Mazeau J 1991 J. Phys. B : At. Mol. Opt. Phys. 24, 1917

[16] Berakdar J and Klar H 1993 J. Phys. B : At. Mol. Opt. Phys. 26 4219

[17] Dorn A, Kheifets A S, Schröter C D, Najjari B, Höhr C, Moshammer R and Ullrich J, 2001 Phys Rev Lett, submitted

[18] Joulakian B and Dal Cappello C 1993 Phys. Rev. A 47 3788

[19] Dal Cappello C and Le Rouzo H 1991 Phys. Rev. A 43 1395

[20] Byron F W Jr and Joachain C J 1989 Physics Reports 179 211

[21] Pochat A, Tweed R J, Peresse J, Joachain C J, Piraux B and Byron F W 1983 J. Phys. B : At. Mol. Phys. 16 L775

[22] Rösel T, Dupré C, Röder J, Duguet A, Jung K, Lahmam-Bennani A and Ehrhardt H 1991 J. Phys. B : At. Mol. Opt. Phys. 24 3059

Caption to figures

Figure 1. (e,3e) fivefold differential cross sections (5DCS) for coplanar double ionization of helium at an impact energy E₀ = 1099 eV, momentum transfer K = 0.45 au (q_a = 1.1°), and equal ejected energies E_b = E_c = 10 eV. The momentum transfer direction is indicated by the bold arrow in panel (a). One electron is detected at a fixed angle, q_fix, shown by the thin arrow and the labeling, while the second electron is mapped in the plane. Experiments are shown as full circles, and the error bars represent one standard deviation statistical error. Full line : CCC results. Dashed line : 3C results. Dotted line : C4FS results with a Hylleraas initial state wavefunction, except in (k) and (v) where a Slater wavefunction is used. The experimental data are obtained on the same relative scale, but for the sake of clarity they are here normalized to the CCC results using different scaling factors, as indicated on each diagram. The absolute scale shown is the CCC one, and is given in 10^-4 atomic units. Similarly, the 3C and C4FS results are renormalized to the CCC ones, also using different scaling factors, as indicated on each diagram.

Figure 2. As for figure 1, (e,3e) 5DCS at E_b = E_c = 10 eV. The experimental data and the CCC results obtained at two q_fix angles which are symmetrical with respect to K direction are here superimposed (q_fix<180° : full circles and full curve. q_fix>180° : open circles and dashed curve.) As in figure 1, the CCC absolute scale is used. For the scaling, the experimental data have been divided by the following factors, respectively from (a) to (f) : 1; 1; 2; 1.6; 2.5; 2.

Figure 3. (e,3e) cross sections in the fixed mutual angle mode, q_bc (see text). Full circles : experiments. Full line : CCC results. Dashed line : 3C results divided by 25 in (a) and (b) and multiplied by 4 in (c). (a) : q_bc = 180°, and the dotted line is a polynomial fit to the experimental data used to guide the eyes; (b) : q_bc =140°; (c) : q_bc = 40°, and in addition the dotted line represents CCC results at q_bc = 0° magnified by 10. Experimental results are normalized to CCC by multiplying them by 1 in (a) and by 7 in (b). Kinematical parameters as in figure 1.

Figure 4 . (a) : (e,3e) cross sections in the symmetric geometry mode, q_b = - q_c (see text). Full circles : experiments. Full line : CCC results. Dashed line : 3C results divided by 4.5. Dotted line : C4FS results divided by 25. Kinematical parameters as in figure 1. (b) The corresponding ion recoil momentum as a function of q_b.