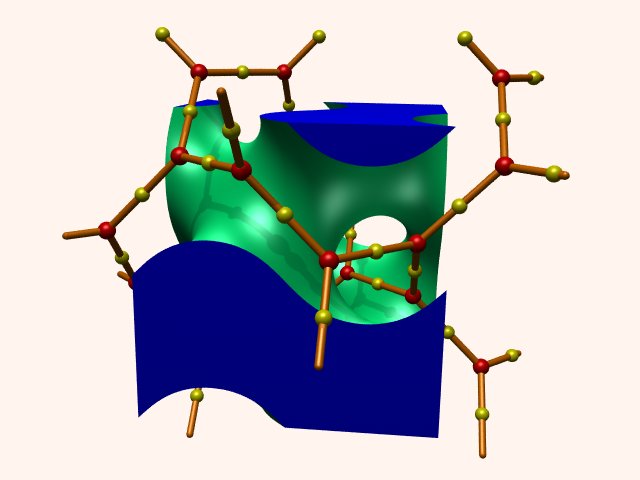
The Gyroid triply-periodic labyrinth
A
homogeneous three-coordinated labyrinth where maxima of the Euclidean
distance map are the midpoint of edges and not the nodes of the network
A mathematical model
labyrinth with a well-defined three-connected network and the peculiar
property that the nodes of the network are inflection points (rather
than maxima) of the Euclidean distance map whereas the maxima are
located at the mid-points of the edges. The Gyroid labyrinth is
periodic in three dimensions, symmetry and it is very homogeneous in
terms of channel diameter variations. The interface between solid and
pore space is a minimal surface.
Description
... under construction ....
What is pathological about it?
The Gyroid is remarkable in that there is no doubt that the network shown above is the
correct homotopy-equivalent network [2], yet the nodes of the network
(red spheres) are not the widest points of the network. The widest
points are at the mid-points of the edges (yellow spheres). This is all
the more unusual in that the Gyroid is one of the most homogeneous
labyrinthine space partitions of its class [2,3].
References
[1] A. Schoen, Infinite Periodic minimal surfaces without self-intersections, Technical Report, NASA (1970)
[2] G.E. Schroeder, S.J. Ramsden, A.G. Christy, and S.T. Hyde, Medial Surfaces of hyperbolic structures, European Physical Journal B, 35, 551-564 (2003)
[3] G.E. Schroeder, Skeletons in the labyrinths, PhD thesis, Australian National University, Canberra, Australia (2005)
Datasets
The following data sets represent the cubic translational
unitcell, in I4(1)32 space group, of the Gyroid labyrinth. Periodic
boundary conditions can be applied in all three directions.
The dataset is generated by creating a triangulation of the Gyroid
interface (from Weierstrass integration) in its unit cube 0 < x,y,z
< 1. Then all points on a grid of n3 points that are on
the positive side of the surface (in normal direction) are set to 1,
all others to 0. The points on that grid are {(i+0.5)*dx, (j+0.5)*dy,
(k+0.5)*dz} with i,j,k = 0, ..., n-1. The grid values are then written
to the data file.
Gyroid triply-periodic labyrinth (n=50)