
The local intrinsic 2D symmetry of these surfaces is a hyperbolic group with orbifold symbol *246. This group is generated by three reflections: R1, R2, R3, in lines that bound a hyperbolic triangle with angles pi/2, pi/4, and pi/6, and satisfy the following identities:
The translation subgroup has orbifold symbol ooo (a genus-3 surface) and has generators:
We find all symmetries that are compatible with these two groups by computing the subgroup lattice of *246/ooo (using the computational discrete algebra package GAP).
See the paper 2D hyperbolic groups induce three-periodic euclidean reticulations for more details.
The database is accessed either through a list of subgroups, or by interacting with a graph of the subgroup lattice that shows the maximal subgroup relations between the 131 different conjugacy classes of subgroups. The link takes you to a high-resolution image map with active nodes that point to more information about that particular subgroup. The graph layout was generated using GraphViz.
Each subgroup record has basic information such as index and conjugacy class size, and two images of the symmetry action in the hyperbolic plane. These images are based on the Poincare disk model of hyperbolic space. The left image colours the underlying *246 triangles according to distinct subgroup domains in a single translational unit. The right image assigns colour to *246 elements that are equivalent under the subgroup action. For example, the *246 group has subdomain and symmetry colourings as follows:
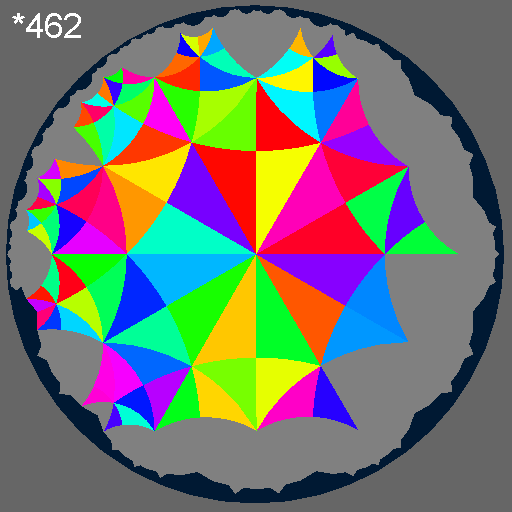 |
 |
An index 3 subgroup has three *246 triangles in each subdomain, and therefore 3 different colours in the symmetry image.
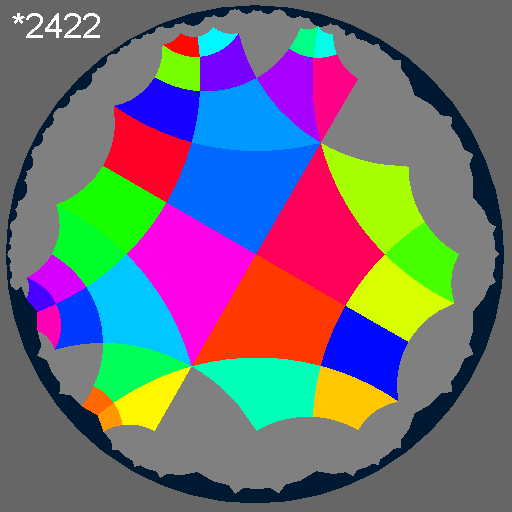 |
 |
The remainder of the subgroup record for this subgroup contains the following information:
| Subgroup number | 123 |
| Orbifold symbol | *2422 |
| Index in *246 | 3 |
| Conjugacy Class Size | 3 |
| Generators in *246/T | R1, R2, R3R2R3, R3R1R3R1R3 |
| Maximal Subgroups | 107 . 101 . 100 . 114 . 106 . 105 . 104 . 110 . 111 . 112 . 113 . 103 . 102 . 109 . 108 . |
The conjugacy class size is the number of subgroups of *246 that are related to this one via conjugacy (i.e. elements g, h, in the two groups are related via the expression g = r^-1 h r for a fixed element r in *246).
The generators listed are elements of the compactified group *246/ooo and will generate the compactified subgroup *2422/ooo. Generators for the infinite group *2422 must include the six translations that generate ooo.
The maximal subgroups are the "children" of the given node in the subgroup lattice.